みなさん、お疲れ様です!超音波検査士けんしんです。
今回は空間分解能に関する問題です。それではさっそく問題をやっていきましょう!
公式は・・・( )
(2)方位分解能・・・超音波ビームと垂直方向の分解能(左右)
公式は・・・( )
(3)スライス幅分解能・・・超音波のスライス幅(ビーム幅)方向の分解能(前後)
要因・・・( )( )( )
(4)マトリックスアレイプローブ
・( )方向にも振動子を配列してある→( )数、( )数がUP!
→駆動列を変えることで( )を変えることができる。
→( )を設けることで電子フォーカスをかけることができる。
→リアルタイムに( )を得ることができる。
・( )は使用されていない
・( )は適していない
公式は・・・(Δx=nλ/2) nλ:パルス幅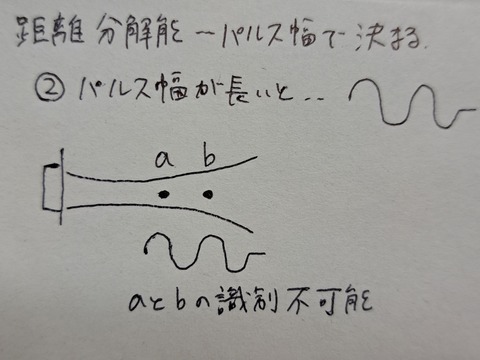
(2)方位分解能・・・超音波ビームと垂直方向の分解能(左右)
公式は・・・(Δy=d/2 ≒ 1.22λ×X/D)

(3)スライス幅分解能・・・超音波のスライス幅(ビーム幅)方向の分解能(前後)
要因・・・(音響レンズ)(波長・周波数)(振動子の幅)
(4)マトリックスアレイプローブ
・(スライス)方向にも振動子を配列してある→(素子)数、(振動子の)数がUP!
→駆動列を変えることで(焦点距離)を変えることができる。
→(遅延時間)を設けることで電子フォーカスをかけることができる。
→リアルタイムに(3D画像)を得ることができる。
・(音響レンズ)は使用されていない
・(連続波)は適していない
平成元年生まれのゆとり世代の臨床検査技師。
趣味は陸上短距離、読書、温泉、特撮(特に平成仮面ライダー)。
仕事では超音波検査したり検体検査したり労働組合したりしています。
2018年に2回の受験を経て超音波検査士認定試験(消化器)に合格。2度受験した経験から、知識を覚えるための勉強や症例レポートの作成には仕事をしながらだと時間が作れなくてかなり苦労しました。
そういった経験からこれから超音波検査を勉強したり超音波検査士を受験したりする人が労力や時間をかけずに勉強できるようにと考え、自分が勉強した際のノートや問題、受験の際に提出した超音波検査実績、最近気になるトピックを公開しています。
超音波検査ができる人が増えたり、超音波検査士取得を目指す人同士がつながれるブログになればいいなと考えています。
今回は空間分解能に関する問題です。それではさっそく問題をやっていきましょう!
~空間分解能の問題~
(1)距離分解能・・・超音波ビームの方向の分解能(深さ)公式は・・・( )
(2)方位分解能・・・超音波ビームと垂直方向の分解能(左右)
公式は・・・( )
(3)スライス幅分解能・・・超音波のスライス幅(ビーム幅)方向の分解能(前後)
要因・・・( )( )( )
(4)マトリックスアレイプローブ
・( )方向にも振動子を配列してある→( )数、( )数がUP!
→駆動列を変えることで( )を変えることができる。
→( )を設けることで電子フォーカスをかけることができる。
→リアルタイムに( )を得ることができる。
・( )は使用されていない
・( )は適していない
↓↓答えは広告の下↓↓
~空間分解能の問題の答え~
(1)距離分解能・・・超音波ビームの方向の分解能(深さ)公式は・・・(Δx=nλ/2) nλ:パルス幅
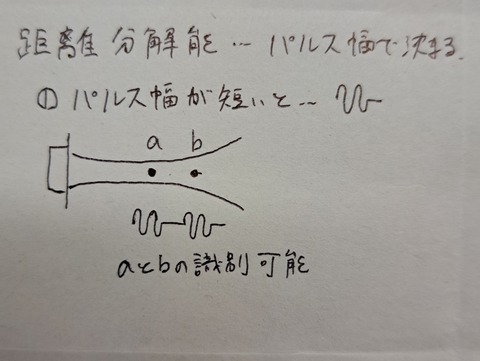
※距離分解能は「パルス幅」で決まる!小さいほど良い!!
・パルス幅が長いと… a、bの識別不可能

(2)方位分解能・・・超音波ビームと垂直方向の分解能(左右)
公式は・・・(Δy=d/2 ≒ 1.22λ×X/D)
d:ビーム幅、λ:波長、D:振動子の開口径、X:振動子からの距離
※方位分解能は「ビーム幅」で決まる!小さいほど良い!!

(3)スライス幅分解能・・・超音波のスライス幅(ビーム幅)方向の分解能(前後)
要因・・・(音響レンズ)(波長・周波数)(振動子の幅)
(4)マトリックスアレイプローブ
・(スライス)方向にも振動子を配列してある→(素子)数、(振動子の)数がUP!
→駆動列を変えることで(焦点距離)を変えることができる。
→(遅延時間)を設けることで電子フォーカスをかけることができる。
→リアルタイムに(3D画像)を得ることができる。
・(音響レンズ)は使用されていない
・(連続波)は適していない
~自己紹介~
超音波検査士けんしん平成元年生まれのゆとり世代の臨床検査技師。
趣味は陸上短距離、読書、温泉、特撮(特に平成仮面ライダー)。
仕事では超音波検査したり検体検査したり労働組合したりしています。
2018年に2回の受験を経て超音波検査士認定試験(消化器)に合格。2度受験した経験から、知識を覚えるための勉強や症例レポートの作成には仕事をしながらだと時間が作れなくてかなり苦労しました。
そういった経験からこれから超音波検査を勉強したり超音波検査士を受験したりする人が労力や時間をかけずに勉強できるようにと考え、自分が勉強した際のノートや問題、受験の際に提出した超音波検査実績、最近気になるトピックを公開しています。
超音波検査ができる人が増えたり、超音波検査士取得を目指す人同士がつながれるブログになればいいなと考えています。

コメント